2つのテストスコアの平均値差を検定するシステム(略称: AVES)です。それぞれの「平均値」「標準偏差」「人数」を入力すれば、2つのテストの正規分布グラフと、「平均値差」「効果量」「検定統計量t値」「P値」「95%信頼区間」「帰無仮説棄却の有無」が出力されます。以下のリンクからアクセスしてください。効果量は「対応のないデータ」と「対応のあるデータ」とで計算式を使い分ける場合があります。ユーザーが適切と考える方を選択してください。
「ユーザーの元データを用いた平均値差の検定」なら、児童生徒ごとの素得点を入力すれば、標準偏差や人数を入力しなくても、効果量を出力します。サンプル数が同じ場合「対応のないデータ」と「対応のあるデータ」の2つの結果が出力されます。
入力データがサーバーなどに送信・収集されることは一切ありません。本ウェブアプリの処理はお使いの端末(ユーザーサイド)のみで行われる仕組みになっています。
開発者:菅原敏(宮城教育大学)・田端健人(宮城教育大学)
公開日:2022.05.22 (ver.1.0.0)
※ このシステムを利用して、論文や記事を作成する場合は、出典を明記してください。例)DS-EFA「平均値差検定システム(ver. 1.0.0)」(https://ds-efa.info/script/cohensd.html)を利用した。
※ 商業利用は禁止します。
平均値差検定システム
- 対応のないデータの平均値差の検定
- 対応のあるデータの平均値差の検定
<画面イメージ>
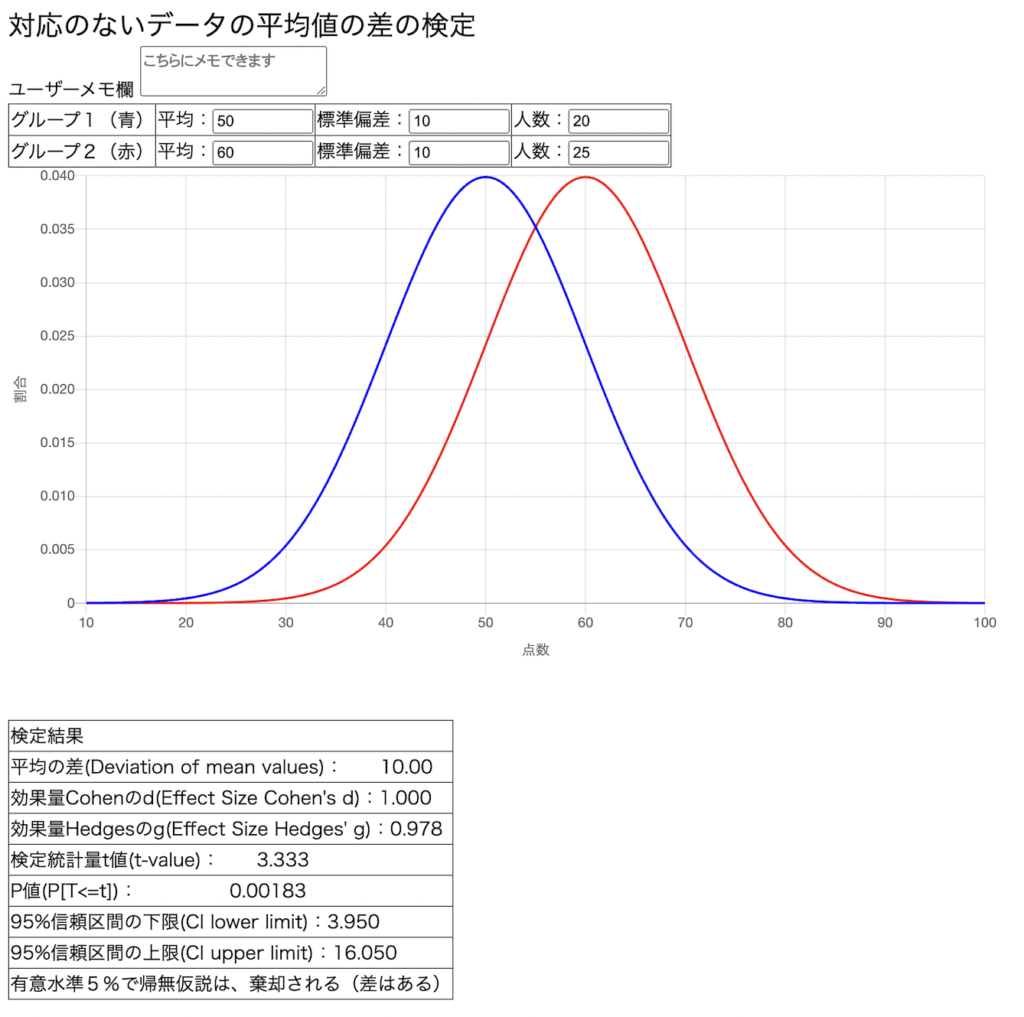
2つのテストの平均値差が、偶然に生じたものかそうでないかを確率的に判断する方法を、一般に「統計的仮説検定」と呼びます。偶然かどうかを判断する際の基準を「有意水準」と呼び、慣例で5%が用いられます。検定によりP値が5%を下回った場合、「統計的に有意な差」とみなし、偶然に生じた差ではないと判断します。偶然に生じた差ではないということは、なんらかの働きかけや事情が作用した結果の差と考えます。この検定が「仮説検定」と呼ばれるのは、「2つの平均値に差はない(同等である)」という「帰無仮説」を立てるからです。P値が5%未満だとこの帰無仮説を棄却し、その対立仮説「2つの平均値には差がある」を採用するという手順です。
ただP値はサンプル数(人数)が多くなれば5%を下回りやすくなるため、実質的な差がなくてもP < 0.05になることがあります。
そこで、平均差の大きさを評価するには、サンプル数の影響をほとんど受けない効果量(Effect Size)など複数の検証が必要です。差の大きさを表す効果量は70種類以上あるとされますが、本システムは代表的な「Cohen(コーエン)のd」と「Hedgesのg」と、対応のある場合の「差得点の効果量」を採用しています。
目安(基準値)には諸説あります。全国学力・学習状況調査の平均差を評価する基準値としては、私たちは以下を提唱しています(2023年7月27日現在)。
d < 0.4(差はない)、0.4≦d < 0.5(小さな差)、0.5≦d < 0.7(中程度の差)、0.7≦d(大きな差)
d = 1.0は、1標準偏差分(偏差値なら10)の差があることを意味します。
効果量は、「対応のないデータ」と「対応のあるデータ」で計算式を変える考え方があります。「対応のないデータ」とは、異なるグループのデータを意味し、例えば6年1組と2組の平均値差の効果量になります。「対応のあるデータ」とは、同一グループのデータで、例えば6年1組の4月と7月のテスト平均値差の効果量になります。「対応のあるデータ」の効果量には2通りの考え方があり、①「対応のない場合」のCohenのdやHedgesのgを使う考え方と、②「得点差の効果量」を用いる考え方があります。①の考えをとるユーザーは本システムの「対応のないデータ」をご利用ください。②の考えをとるユーザーは本システムの「対応のあるデータ」をご利用ください。「ユーザーの元データを用いた平均値差の検定」は、サンプル数が異なれば、「対応のないデータ」結果のみを出力し、サンプル数が同じなら、「対応のあるデータ」の結果も合わせて出力します。対応のある場合のデータは、ID揃えた順序でスコアを入力してください。
「95%信頼区間」は繰り返し信頼区間を求めたときに、95%の割合でこの範囲に真の値が存在することを意味します。もしこの範囲がゼロをまたぐなら、「統計的に有意な差があるとは言えない」と評価します。
効果量の簡単な解説と本システムの数式については、こちらを参照してください。平均値や標準偏差、標本分散や不偏分散をエクセルで計算する方法も解説しています。